[高级数据结构] AVL树

AVL树的定义

空的二叉树是高度平衡的。如果T是以TL和TR为左右子树的非空二叉树，则T是高度平衡的，当：

（1） TL和TR是高度平衡的，并且；

（2） | hL.-hR | <= 1，其中hL和hR分别是TL和TR的高度。

与二叉树的区别：

在插入和删除节点时会对树的其他节点进行调整，保证树仍然处于AVL平衡状态。

AVL树的操作

调整

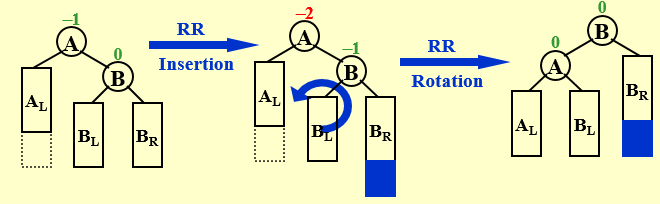
RR Rotation

对于 Trouble Maker 在 Trouble Finder 的右节点的右节点插入导致的 unbalance，需要以 TF 为轴左旋。调整后A是B的左节点，BL是A的右节点，B的左节点是A。

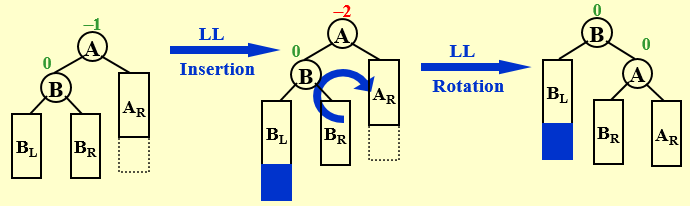
LL Rotation

同RR相反，也需要进行一次单旋。

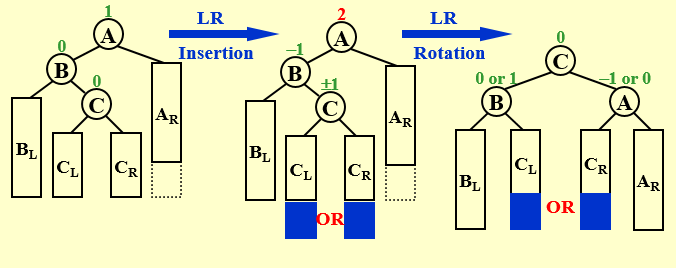
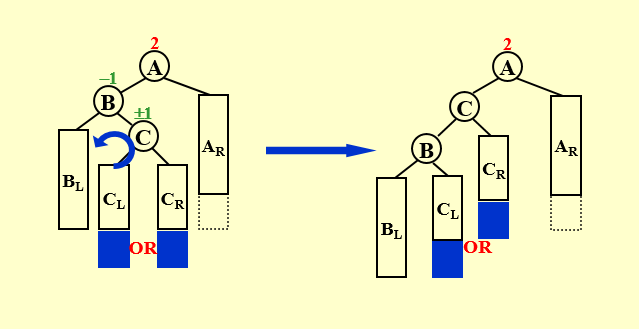
LR Rotation

TM 在 TF 的左节点的右节点下。需要进行两次旋转将左节点的右节点移至原 TF 的位置。

第一次旋转以 TF 左节点为轴往左旋转。

再以 TF 的左节点为轴右旋。

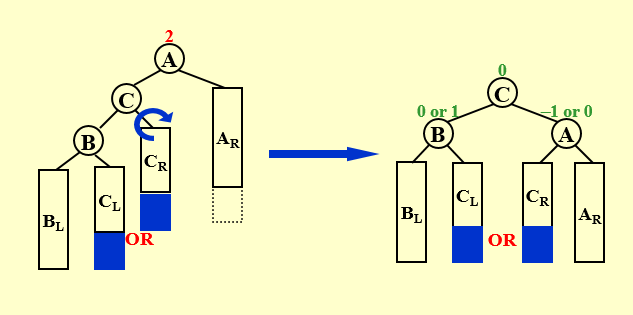
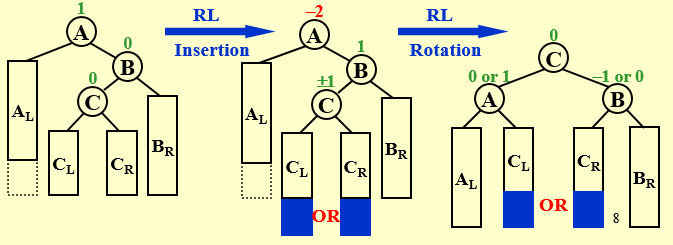
RL Rotation

与LR的情况相反。

相关题目

 If the depth of an AVL tree is 6 (the depth of an empty tree is defined to be -1), then the minimum possible number of nodes in this tree is: (2分)

1. 13
2. 17
3. 20
4. 33

构建代码

//
//  main.cpp
//  AVL tree
//
//  Created by Jeanne Mystery on 2020/3/6.
//  Copyright © 2020 Jeanne Mystery. All rights reserved.
//

#include <iostream>
using namespace std;
class AVLTree{
public:
    int val;
    AVLTree *left;
    AVLTree *right;
    AVLTree( int val ){
        this->val = val;
        this->right = NULL;
        this->left = NULL;
    }
};

AVLTree* LeftRotation( AVLTree* root ){
    AVLTree* temp = root->right;
    root->right = temp->left;
    temp->left = root;
    return temp;
}

AVLTree* RightRotation( AVLTree* root ){
    AVLTree* temp = root->left;
    root->left = temp->right;
    temp->right = root;
    return temp;
}

int getHeight( AVLTree* root ){
    int hl = 0, hr = 0;
    if( root == NULL ){// leaf node
        return 0;
    }
    else{
        hr = getHeight(root->right) + 1;
        hl = getHeight(root->left) + 1;
        return hl > hr ? hl : hr;
    }
}

AVLTree* Insert( int val, AVLTree* root){
    if( root == NULL ){
        AVLTree *temp = (AVLTree*)malloc(sizeof(AVLTree));
        temp->val = val;
        temp->left = NULL;
        temp->right = NULL;
        root = temp;
    }
    else if( val > root->val ){
        root->right = Insert( val, root->right );
        if( getHeight(root->right) - getHeight(root->left) == 2 ){
            if( val > root->right->val ){ //Double R->LeftRotation
                root = LeftRotation(root);
            }
            else{ // RL->RightRotation->LeftRotation
                root->right = RightRotation(root->right);
                root = LeftRotation(root);
            }
        }
    }
    else {
        root->left = Insert( val, root->left );
        if( getHeight(root->right) - getHeight(root->left) == -2 ){
            if( val < root->left->val ){ //Double L->RightRotation
                root = RightRotation(root);
            }
            else{ // LR->LeftRotation->RightRotation
                root->left = LeftRotation(root->left);
                root = RightRotation(root);
            }
        }
    }
    return root;
}

int main(int argc, const char * argv[]) {
    int n;
    //std::cout << "Hello, World!\n";
    cin >> n;
    AVLTree* root = NULL ;
    for( int i = 0 ; i < n ; i++ ){
        int val;
        cin >> val;
        root = Insert(val,root);
    }
    cout << root->val << endl;
    return 0;
}